1. Home
  2. Support
  3. RF design tools
  4. Series and parallel RL/RC network converter

Support

Series and parallel RL/RC network converter

This tool provides real-time and precise data conversion and analysis of series and parallel configurations of resistor-inductor (RL) and resistor-capacitor (RC) circuits to calculate impedance, reactance, and component values.

-

Series to Parallel – RL Network

Series to Parallel – RL Network Image
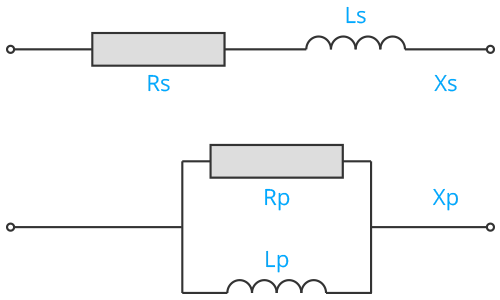
\[ X_L = 2\pi f L \]
\[ R_p = (Q^2 + 1) R_s \]
\[ L = \frac{X_L}{2\pi f} \]
\[ X_p = \frac{R_p}{Q_p} \]
\[ Q_s = \frac{X_s}{R_s} \]
\[ Q_p = \frac{R_p}{X_p} \]

Series to Parallel – RC Network

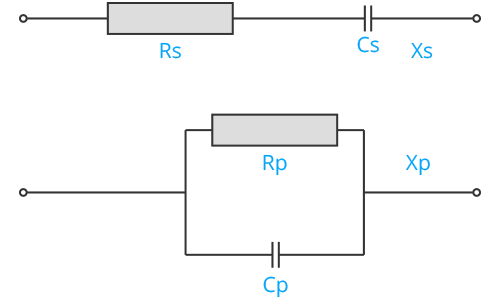
Series to Parallel – RC Network Image
\[ X_c = \frac{1}{2\pi f C} \]
\[ Q_s = \frac{X_s}{R_s} \]
\[ R_p = (Q^2 + 1) R_s \]
\[ X_p = \frac{R_p}{Q_p} \]
\[ C = \frac{1}{2\pi f X_c} \]

Parallel to Series – RL Network

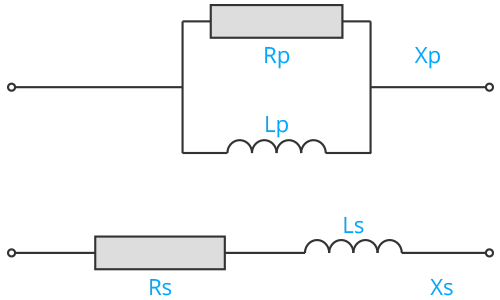
Parallel to Series – RL Network Image
\[ X_L = 2\pi f L \]
\[ Q_p = \frac{R_p}{X_p} \]
\[ R_s = \frac{R_p}{Q^2 + 1} \]
\[ X_s = Q_s \cdot R_s \]
\[ L = \frac{X_L}{2\pi f} \]

Parallel to Series – RC Network

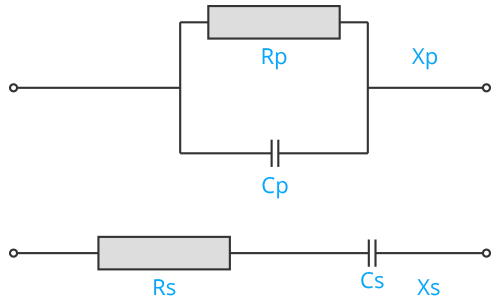
Parallel to Series – RC Network Image
\[ X_c = \frac{1}{2\pi f C} \]
\[ Q_p = \frac{R_p}{X_p} \]
\[ R_s = \frac{R_p}{Q^2 + 1} \]
\[ X_s = Q_s \cdot R_s \]

Input

Output

Input

Output

Input

Output

Input

Output

Disclaimer: Ampleon does not make any guarantees or assurances, whether explicit or implied, regarding the completeness, accuracy, or reliability of the tools available on this web page. Ampleon can not be held liable for any losses or damages, including direct or indirect or consequential damages, that may arise from or be related to the use of these tools.